CCSE Home

Home

Research

Publications

People

AMReX

MODS

Combining Data and Simulation to Predict the
Behavior of Complex Systems

Introduction

Predicting the behavior of complex physical systems is a key requirement for many important DOE applications. However, incomplete physical models and uncertain parameters limit the predictive capability of even high fidelity simulations. Model and parameter identification are typically done by finding models and parameter sets that accurately predict the results of controlled experiments. This often involves a combination of computation and optimization.

Senior Investigators

Project Goal

The goal of this project is to develop new tools that allow us to use data from multiple experiments of different kinds in conjunction with simulation. It has become clear that traditional simulation and sampling methods do not suffice. The constraints that experiments put on parameters are ill conditioned and complex. Simulating highly nonlinear experiments is so slow that huge numbers of samples are not practical.

Measurements often reflect a complex, uncertain relationship between the system state and measured quantities. For example, laser diagnostic measurements of a chemical species in a reacting flow are modulated by state-dependent quenching corrections. Observations from cosmological surveys require modeling of photometric redshifts, corrections for telescope focal plane distortions, and a number of other systematic effects. In some cases, the combination of imprecisely defined experiments and complex dynamics means that it is appropriate to consider only statistical properties of the experiments, not a detailed trajectory.

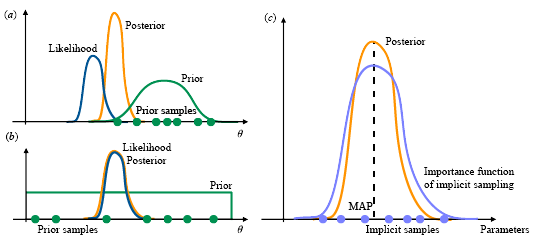
Approach

Our overall approach is based on Monte Carlo sampling within a Bayesian framework. Monte Carlo (MC) sampling provides a numerically sound implementation that respects the strong nonlinearity in the target applications. Our hierarchical approach in this project is based on a combination of implicit sampling (IS), Markov chain MC (MCMC), and reduced-order models (ROMs), with a focus on application to complex, high dimensional problems.

In Implicit Sampling, sample generation is guided by the solution of an optimization problem that is based on the target model; this helps to identify regions of high probability with respect to the posterior (see Implicit Sampling inset below). For MCMC, we use techniques based on parallel marginalization to reduce correlation time in the sampling process, and use an affine-invariant sampling algorithm to improve the overall efficiency when the parameters span orders of magnitude in scale and variation. Reduced order models will play an increasingly important role in building a hierarchy of targets, particularly when the targets span a large range of computational complexities, and when observables are complex functions of the simulated state variables.

Implicit Sampling

A "Prior" distribution for a parameter is one that is consistent with previous knowledge. The "Likelihood" represents the parameter distribution that is consistent with the new information. Sampling will create the "Posterior" distribution that will be consistent with all the data. In the (desireable) case that the new data strongly informs the parameters, there are several conditions that make sampling the posterior a difficult task.

In (a), the prior and likelihood are peaked and well-separated. A set of samples based on the prior distribution will rarely result in a good fit to the new data. Similarly, a uniformly distributed sample set (b) will generate a high fraction of unlikely samples. With enough samples, the posterior in either case will eventually be characterized, but with catastrophically poor efficiency. Implicit Sampling rather proposes a distribution of samples based on a local model of the posterior (c). Ideally, the local model is centered near the peak value of the likelihood and is just broad enough to sample the structure of the distribution without wasting effort sampling regions of low probability. However, this added efficiency is not free. IS requires that one be able to predict a good generic model for the posterior, and then be able solve the associated constrained optimization problem to set the parameters of the fit. We are currently exploring the feasibility of such an approach for realistic applications, by combining IS with the other approaches discussed above into an iterative adaptive sampling framework.

As an example, combustion chemistry models are constructed and optimized with respect to available experimental data; typically including volumetric reactors (such as calormetric bombs, flow reactors, shock tubes), and counterflowing flame systems -- all of which are low-dimensional idealized configurations providing fairly well-characterized data for limited parameter ranges. However the resulting "validated" combustion models are then applied to a wide range of systems, from zero-D and steady systems to fully turbulent combustion environments. Historically, there has been very little feedback from the more practical combustion systems to the improvements of the underlying models.

Ultimately, we would like to combine all of these technologies into an extensivle hierarchical adaptive sampling scheme for high-dimensional parameter space, where we can directly exploit the wide range of computational expense associated with zero-D systems through turbulent 3D reacting flow systems. The ultimate goal is to create the methodology to incorporate increasingly complex, realistic and relevant experimentally observable data into the development and improvement of the fundamental models that underpin the computational predictions of complex multiphysics systems.

Applications

  • Combustion

  • Cosmology

  • Transport in thin-film polymers

  • Geosciences

    • Contact

    For more information, contact John Bell or Marc Day.