CCSE Home

Home

Research

Publications

People

AMReX

MODS

Spectral Deferred Correction Methods

Spectral Deferred Corrections is an iterative strategy for constructing higher-order temporal evolution schemes for ODEs and PDEs. The iterative nature of SDC methods can be exploited to create higher-order methods for stiff systems in which operator splitting is employed to avoid the computational cost of coupled implicit processes. This multi-implicit (MISDC) strategy is being applied to reacting gas dynamics simulations in which both the reaction and diffusive terms are treated implicitly but independently. Recent work has also considered ways in which these decoupled implicit solves can be done concurrently.

SDC methods are also the key component of the PFASST parallel in time method PFASST. In the PFASST algorithm, multi-level SDC iterations are performed on multiple time slices and in parallel with corrections to the initial solution on each time slice and MLSDC level communicated after each deferred correction sweep.

Other projects underway include evaluating the efficiency of SDC methods for geophysical flows, constructing higher-order projection methods for the incompressible Navier-Stokes equations, and building SDC based Magnus integrators for isospectral flow problems. See below for more project details

☞ For more information, contact Michael Minion [email protected].

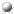Concurrent Implicit Spectral Deferred Correction Methods

Many multiphysics simulations involve computational components that are difficult to scale on extreme-scale hardware (e.g. linear solvers). We developed an iterative integrator based on SDC, referred to as Concurrent Implicit Spectral Deferred Correction (CISDC), that couples concurrently evaluated physics kernels, thereby injecting a new axis of algorithmic parallelism. The new coupling strategy intertwines asynchronous evaluation of tightly coupled processes in multiphysics applications. We demonstrated favorable performance of the new CISDC scheme for simulating low Mach number combustion, featuring stiff coupled chemistry and transport.

☞ For more information, contact Francois Hamon [email protected].



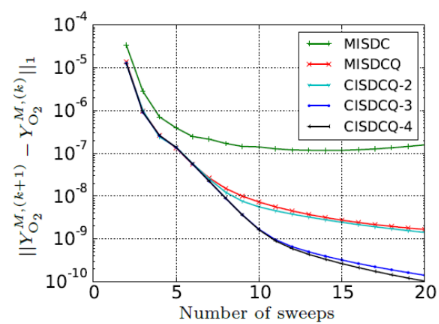
Evaluating SDC for Geophysical Flow Test Cases

Efficient high-order time integration is necessary to capture the complex processes involved in atmospheric flows over long periods of time. Multilevel iterative time integrators like Multi-Level Spectral Deferred Correction (MLSDC) shift the computational work to a coarse representation of the problem and reduce the time-to-solution. We developed a high-order numerical scheme combining MLSDC and the global spherical harmonics transform to efficiently solve the shallow-water equations on the sphere. We demonstrated the efficiency and high-order accuracy of the new numerical scheme using the standard benchmark test cases used in the atmospheric modeling community. This effort represents a first step towards a successful parallel-in-time integration of the full atmospheric dynamics using PFASST.

☞ For more information, contact Francois Hamon [email protected].

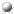Spectral Deferred Pressure Corrections

A new method for the temporal integration of the incompressible Navier-Stokes equations in bounded domains has recently been developed. The Spectral Deferred Pressure Correction method (SPDC) applies semi-implicit SDC sweeps to an auxiliary variable projection formulation of the equations and the pressure approximation is corrected after each sweep. This temporal method has been coupled with a higher order discontinuous Galerkin spatial approximation and variants of up to 8th-order accuracy have been demonstrated on problems with constant Dirichlet boundary conditions. For time-dependent boundary conditions, a form of order-reduction occurs reducing the observed order by one half.

☞ For more information, contact Michael Minion [email protected].


F.P. Hamon, M.S. Day, M.L. Minion, "Concurrent Implicit Spectral Deferred Correction Scheme for Low-Mach Number Combustion with Detailed Chemistry", submitted for publication. [arxiv]

R.W. Grout, H. Kolla, M.L. Minion and J.B. Bell, "Achieving algorithmic resilience for temporal integration through spectral deferred corrections," to appear in Commun. in Appl. Math. and Comput. Sci. [arxiv].

W. Pazner, A. Nonaka, J. B. Bell, M. S. Day, and M. L. Minion, "A High-Order Spectral Deferred Correction Strategy for Low Mach Number Flow With Complex Chemistry," Combust. Theory Modelling, [DOI] , 2016. [pdf]

M. Minion, R. Speck, M. Bolten, M. Emmett, and D. Ruprecht "Interweaving PFASST and parallel multigrid", SIAM J. Scientific Computing, 37(5), pp. S244-S263, 2015.

R. Speck, D. Ruprecht, M. Minion, and R. Krause, "Inexact Spectral Deferred Corrections", Domain Decomposition Methods in Science and Engineering XXII, 104, pp. 127--133, 2015.

R. Speck, D. Ruprecht, M. Emmett, M. Minion, M. Bolten, and R. Krause "A multi-level spectral deferred correction method", BIT Numerical Mathematics, 2014 [arxiv].

M. Emmett and M. Minion "Efficient implementation of a multi-level parallel in time algorithm", Proceedings of the 21st International Conference on Domain Decomposition Methods, DD21, , 98, 359-366, 2014.

A.S. Almgren, A.J. Aspden, J. B. Bell, and M. L. Minion, "On the Use of Higher-Order Projection Methods for Incompressible Turbulent Flow", SIAM J. Sci. Comput., 35, 1, B25-B42, 2013. [pdf]

R. Speck, D. Ruprecht, R. Krause, M. Emmett, M. Minion, M. Winkel, and P. Gibbon, "A massively space-time parallel N-body solver", Proceedings of the International Conference on High Performance Computing, SC'12, 92:1-11, 2012.

R. Speck, D. Ruprecht, R. Krause, M. Emmett, M. Minion, M. Winkel, and P. Gibbon, "Integrating an N-body problem with SDC and PFASST", Proceedings of the 21st International Conference on Domain Decomposition Methods, DD21, 2012.

A. Nonaka, J. B. Bell, M. S. Day, C. Gilet, A. S. Almgren, and M. L. Minion, "A Deferred Correction Coupling Strategy for Low Mach Number Flow with Complex Chemistry", Combustion Theory and Modelling, vol. 16, no. 6, pp. 1053-1088, 2012. [pdf]

M. Emmett and M. Minion "Toward an efficient parallel in time method for partial differential equations", Commun. in Appl. Math. and Comput. Sci, 7(1), 105-132, 2012.