B. Merriman,
F. Najmabadi,
R. W. Conn
Abstract
The classical plasma electron heat flux can greatly overestimate the physical heat flux when the electron mean-free-path becomes long compared to the electron temperature gradient scale length. For fluid modelling of plasmas, a common remedy is to apply an artificial ``flux limiter'' that keeps the heat flux at a physically reasonable value in this long mean-free-path regime. The limiter is not derived from first principles and it introduces a poorly understood free parameter into the model. We study the effect of this parameter in our divertor plasma models to understand how it influences the computed solution. We investigate regimes of both short and long mean-free-path and consistently find large parameter sensitivity. Thus, without additional experimental or theoretical guidance in the choice of flux-limit parameter, flux limiting does not appear to provide an acceptable basis for predictive plasma fluid modelling.
1. Background
Early experiments with laser-heated plasmas demonstrated that the classical
expressions for thermal conductivities lead to significantly overestimated
electron heat fluxes in
regimes of long mean-free-path. This observation led to the flux-limit
models which are employed
to study and predict divertor behavior. Typically, flux
limiters impose a maximum allowable heat flux of the form,
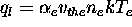(where
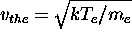is the electron thermal velocity,
and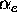 
is an arbitrary constant such that 
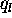remains
less than the flux of thermal energy that could be carried by
the electrons moving at their thermal speed). The limited heat flux is
written as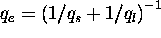 
,
which is an arbitrary interpolation between the free-streaming and
Spitzer values (here,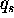 
is the classical Spitzer heat flux). The
flux-limit parameter,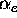 
, is adjusted according to some
application-specific kinetic modelling or experimental data. For tokamak edge
plasma modelling, values for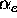 
range typically from .12 to .50[1].
In addition to flux-limiting models, there has been considerable
theoretical effort to develop nonlocal heat conduction models[2].
Reference 3 includes a critique of a large class of such models; we focus here
only on the local flux-limited models widely used in divertor modelling.
We have developed a 1D fluid model[4,6] which uses the above flux-limiter expression in simulating experimental data taken from a variety of plasma conditions in the PISCES-A facility at UC San Diego. Using this model, we perform sensitivity analyses to characterize how the flux-limit parameter influences the computed solutions.
2. PISCES-A Model and Results
The PISCES-A facility has been described in detail elsewhere[5]. Briefly,
PISCES-A is a linear device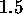 
m in length and 10 cm in diameter
with plasma confined radially by a solenoidal magnetic field. Ions are
not heated and remain near 2 eV (their Franck-Condon energy).
The plasma regime for the electrons is in the range characteristic of divertor plasmas. In the
gas-target experiments[6],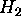 
is puffed into the system near
the target, causing the plasma density to detach fully from the target and
the electron temperature to collapse. Plasma detachment reduces the target heat load by more than 97%,
and thus may be an attractive regime for divertor operation.
The model of Reference 4 and 6 describing these gas-target experiments employs
classical fluid plasma transport parallel to the magnetic field for plasma
density, plasma momentum and electron temperature, except that the electron heat flux is limited as described above, with flux-limit parameter,
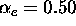. Radial transport effects are simulated by assuming radial
scale lengths and diffusivities. Neutral H and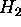 
transport are modeled
by diffusion. For the high-pressure ``gas-target'' regime (induced by strong
external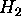 
puffing), we performed sensitivity studies for 
.
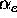The resulting profiles are shown in Figure 1 for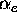 
through the range 
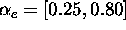. In these results, the
target is toward the left and the inlet is toward the right of the 100 cm model domain.
We also simulated a low-pressure PISCES-A case (no external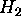 
puffing). Our model successfully reproduces measured data for this case only
after decreasing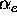 
to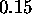 
. The profiles obtained by varying
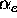through the range, 
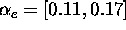, are shown
in Figure 2.
In Figure 3 we plot the ratio, R, of the mean-free-path for Coulomb collisions to electron temperature gradient scale length for the high- and low-pressure PISCES-A experimental data (based on the computed solutions that best represent the experimental data). Where R exceeds unity the classical heat flux significantly overestimates the physical heat flux, and the flux limiter must significantly impact the fluid model.
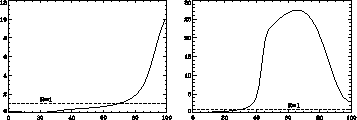
Figure 3: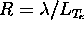 
for gas-target (left) and low-pressure (right) PISCES-A models.
In the high-pressure experiment, the mean-free-path is smaller than the
temperature scale length (R<1) over most of the domain, except near
the inlet. Even so, Figure 1 shows that variations in the flux
limit parameter have remarkable effects on the solution profiles. In the
low-pressure case, R>1 over a large part of the domain, and the sensitivity
of the solution profiles to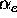 
is even more pronounced. In the
latter case, there is a strong relation between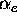 
and the resulting
predicted target temperature. It is clear from the both figures that small
changes in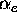 
, will ``tune'' the computed results. In applications
of a similar model to a high power gas-target tokamak divertor regime, we further found that the relation between variations in
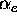and the resulting plasma profiles was not easily
predictable. This makes it difficult to provide generally useful
guidelines about the effect of the flux limit on
the computed solutions.
3. Simple Analytic Model
A simple model for electron heat transport can be constructed to illustrate
some basic effects of the limiter. We start from parallel transport
equations for plasma density, momentum and energy. Assuming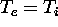 
and neglecting sources
we can satisfy the steady state continuity and momentum
equations with zero flow velocity and
a constant plasma pressure. The steady heat transport equation
then reduces to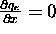 
.
This equation can be integrated twice to obtain
,
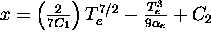where we have absorbed all the physical constants into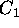 
, 
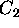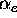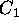and 
(
and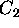 
may be set with Dirichlet boundary conditions). In
Figure 4,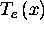 
is plotted for a range of 
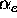with arbitrary 
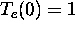and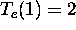 
. Note that there exists a critical
,
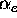below which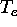 
cannot simultaneously satisfy the boundary values and\
remain single valued in x (so as to admit a physically relevant solution).
In fact, for any ``flux-limiting'' model, if the conductivity,
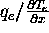, is strictly
an increasing function of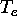 
and if 
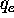remains bounded as
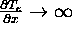, then there may be no solution which
satisfies both boundary conditions for an arbitrarily large heat flux.
EPS/toyFl.epsFlux limit variations in simple analytic model.toyFl.4
Note that the limited heat flux becomes an increasingly weaker function of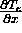 
as the local temperature gradient increases; this in turn
requires much steeper gradients to carry the heat flux as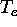 
(and
thus the conductivity) decreases. In contrast, kinetic effects in the physical
system tend to relax local gradients because hot particles tend to
carry heat further into cool regions.
In the results for PISCES-A (Figures 1 and 2),
decreasing
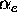leads to more steep temperature profiles, as expected from the
simple model. Additionally, our models exhibit a threshold, beyond which
steady solutions no longer exist, also as predicted by the simple
arguments above. In the low-pressure regime, we could find no steady
solutions for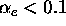 
.
4. Conclusions
We have shown that details of the particular flux-limiter implementation have significant impact on computed divertor plasma solutions in 1D. We analyzed a simple model for the limiter and found that it may not admit physically realistic solutions. Profiles computed with these flux-limited models can be ``tuned'' strongly via minor variations in the arbitrary parameter of the model. Based on this behavior, we conclude that flux-limiting does not provide an acceptable alternative to more detailed (kinetic) modelling for predictive plasma applications. Use of flux limiters should be accompanied by sensitivity studies such as those presented here, and may require additional experimental or theoretical input to select a proper value of the flux-limit parameters for predictive modelling, even when modelling within a restricted regime of plasma parameters.
References
R. H. Cohen, et al.,
Contrib. Plasma Phys. 34 (2/3), 198 (1994)
J. F. Luciani, et al.,
Phys. Rev. Lett. 51, 1664 (1983)
M. K. Prasad and D. S. Kershaw,
Phys. Fluids B 1 (12), 2430 (1989)
M. Day, Ph.D. Thesis, UCLA (1995)
D. M. Goebel, et al.,
J. Nucl. Mat. 121, 27 (1984)
L. Schmitz, et al., Physics of Plasmas
8, 3081 (1995)
