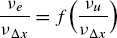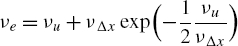Home |
Research | Publications |
People |
Software |
Links |
Downloads |
Implicit Large Eddy Simulations
Introduction
Implicit Large Eddy Simulation (ILES) methods employ second-order or higher finite-volume schemes to capture the inviscid cascade of kinetic energy through the inertial range, while the inherent numerical dissipation acts as an implicit subgrid model, forming a natural form of LES. However, the absence of a physical viscosity prohibits conventional characterization of these methods, specifically how kinetic energy is dissipated at the grid scale and how to define a relevant Reynolds number.
Analysis
Kolmogorov's 1941 papers achieve this characterization for real-world viscous fluids in terms of a universal equilibrium range determined uniquely by the rate of energy dissipation and the physical viscosity.
An analogous approach can be taken for ILES. Assuming the resolution is sufficiently high (analogous to the Reynolds number), the characteristic parameters are the energy dissipation rate, the integral length scale, and the computational cell width (which replaces viscosity).
Therefore, dimensional analysis can be used to write an expression for the kinetic energy spectrum in an ILES fluid
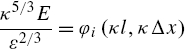
The first similarity hypothesis can be stated such that for scales much smaller than the integral length scale, the turbulent statistics are of universal form determined uniquely by the energy dissipation rate and the computational cell width.
Similarly, the second similarity hypothesis can be stated such that for scales within the universal equilibrium range that are larger than the computational cell width, the turbulent statistics are independent of the cell width. Therefore, an inertial range exists for an ILES fluid.
The important point is independence from the small scales means that the inertial range in an ILES fluid should be consistent with that of a real-world viscous fluid.
An effective Kolmogorov length scale can be derived, which dimensional analysis suggests should follow the relation
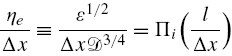
for some dimensionless function Πi, where
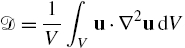
is a measure of the velocity gradients in the flow.
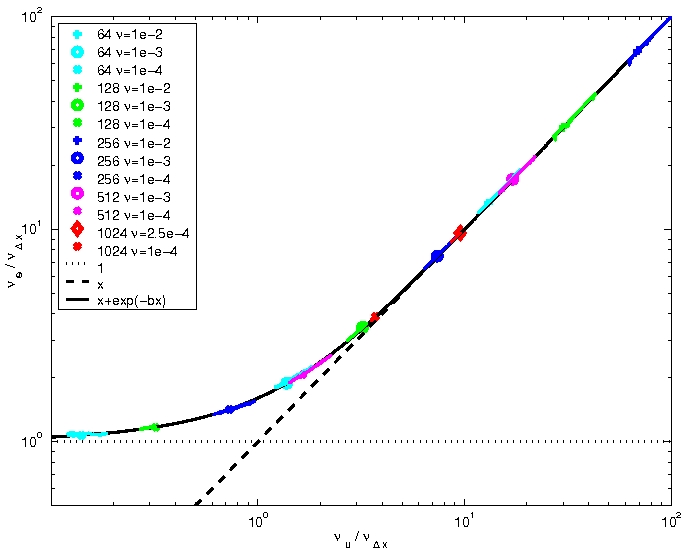
Complete similarity suggests that this function Πi is a universal constant for a given numerical scheme, but this was shown not to be the case.
Results
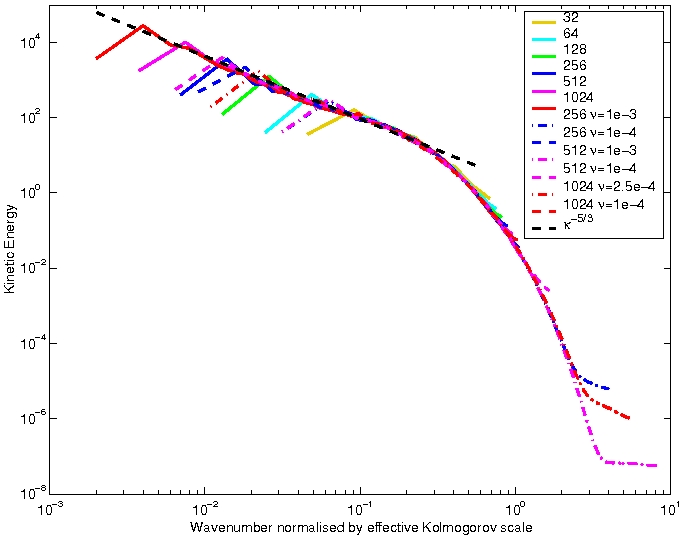
The above theory was tested in the context of maintained homogeneous isotropic turbulence using IAMR. Simulations were run from 323 to 10243 with a time-dependent zero-mean forcing term consisting of superimposed low wavenumber Fourier modes. A series of viscous simulations were also run for comparison.
In each case, it was found that the value of Πi settled down to a constant once the turbulence was fully-developed. A weak non-linear dependence on Reynolds number was observed. (See the paper for more detail).
|
By normalizing the kinetic energy spectrum by the energy dissipation rate and the effective Kolmogorov length scale, a very good collapse of the data was observed (left - click for larger image). Solid lines denote ILES simulations, dashed lines denote viscous simulations, and the dashed black line denotes a five-thirds decay. The extent of the inertial range was shown to correlate with the effective Reynolds number, consistent with the viscous simulations. |
|
A series of underresolved viscous simulations were also conducted to understand the behavior of the scheme when marginally resolved. Dimensional analysis suggests that the effective viscosity should vary according to  for some dimensionless function, which the figure on the right (click for larger image) suggests is in good agreement with  |
|
Please refer to the paper for more details.
Any questions should be directed to Andy Aspden.
References
A. J. Aspden, N. Nikiforakis, S. B. Dalziel and J. B. Bell. "Analysis of Implicit LES Methods" Communications in Applied Mathematics and Computational Science, Volume 3, pp.103-126, 2008. [CAMCoS]