Modeling of incompressible and low-speed flows has become one of the cornerstones of the simulation capability of the Center for Computational Sciences and Engineering (CCSE). This capability has been the springboard for CCSE's combustion modeling capability, as well as useful in itself for explorations of incompressible, nonreacting turbulent flow, as shown below.

The algorithmic complexity of AMR algorithms is significantly higher for low-speed as opposed to fully compressible flows. The equations of inviscid gas dynamics are systems of conservation laws, purely hyperbolic in character. The equations governing incompressible flow, by contrast, include hyperbolic equations governing advection, parabolic equations for the Crank-Nicolson discretization of diffusing quantities, and elliptic equations to enforce the velocity divergence constraint. The method we use to solve these equations is based on a projection formulation in which we first solve advection-diffusion equations to predict intermediate velocities, and then project these velocities onto a space of approximately divergence-free vector fields. Our treatment of the first step uses a specialized second-order upwind method for differencing the nonlinear convection terms that provides a robust treatment of these terms suitable for inviscid and high Reynolds number flow. Density and other scalars are advected in such a way as to maintain conservation, if appropriate, and free-stream preservation.

Implicit Large Eddy Simulation

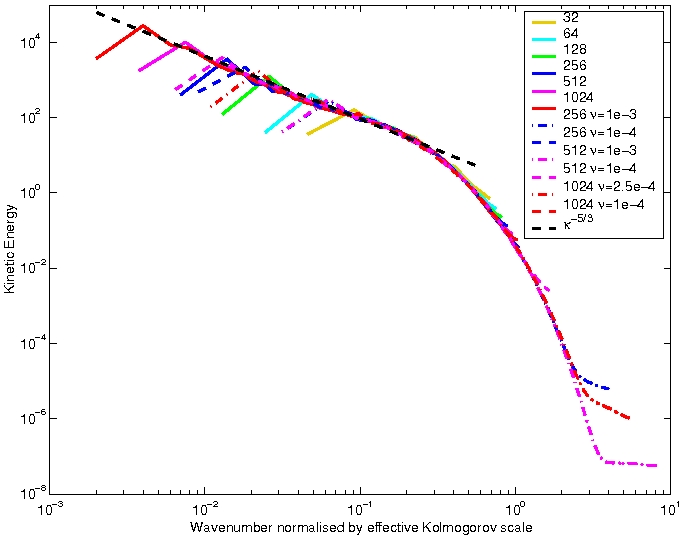
Implicit Large Eddy Simulation (ILES) methods employ second-order or higher finite-volume schemes to capture the inviscid cascade of kinetic energy through the inertial range, while the inherent numerical dissipation acts as an implicit subgrid model, forming a natural form of les. However, the absence of a physical viscosity prohibits conventional characterization of these methods, specifically how kinetic energy is dissipated at the grid scale and how to define a relevant Reynolds number. In this paper, we present an analysis of the behavior of ILES schemes and propose a straight-forward approach to evaluate the effective Reynolds number. We also consider the situation of marginally resolved DNS simulations. The analysis is then tested against simulations of maintained homogeneous isotropic turbulence and the Taylor-Green vortex.

More information can be found here...

Please direct any questions to Andy Aspden.

Turbulent Jets with Off-Source Heating

These simulations look at the entrainment behavior of turbulent jets subject to off-source heating. The still on the left (and the animation mpeg 57MB - right click and select "Save" if you have problems playing the movie) shows a tracer injected with the jets. The jet on the left is unheated. Three different heating rates were applied (increasing to the right) in a narrow horizontal band between 20 and 28 nozzle diameters from the source.

More information can be found here...

Please direct any questions to Andy Aspden.

Three-dimensional Variable Density Incompressible Shear Layer

One of our early calculations using the IAMR methodology was of a time-evolving three-dimensional variable density shear layer. The figure here is a three-dimensional rendering of vorticity; green is the maximum value, and the background black is the absence of vorticity. The problem specification models the classic experiments performed by Brown and Roshko (1974) to study the effects of density variation on low speed shear layers. We can see the essentially two-dimensional roll-up of the vortex sheet as well as the spanwise structure induced by a three-dimensional perturbation of the inflow data designed to mimic a mild "flutter" of the splitter plate used in experiments.

Although the grids are not shown in this image, this calculation was performed adaptively, on a DEC Alpha workstation. In this calculation the density interface and subsequent roll-up are captured at the finest resolution, while the regions near the boundary are at coarser resolution. The computational results were in agreement with experimental data for both the visual spreading rate and the mean profiles of velocity.

Reference

A. S. Almgren, J. B. Bell, P. Colella, L. H. Howell, and M. L. Welcome, ``A Conservative Adaptive Projection Method for the Variable Density Incompressible Navier-Stokes Equations,'', J. Comp. Phys., 142, pp. 1-46, 1998. [ps.gz]