
Turbulence-Flame Interactions in Type Ia Supernovae
Introduction
The complex small-scale dynamics of turbulent thermonuclear flames are essential
to understanding Type Ia supernovae (SN Ia) explosions. In this
paper
we use three-dimensional simulations to examine the interaction of turbulence
with a thermonuclear carbon-burning flame.
The Reynolds number of turbulence typical of a SN Ia is around 1014
so it is infeasible to simulate the entire kinetic energy cascade.
We rely on the ILES properties of our numerical scheme to simulate just the
portion of the inertial range that can interact with the length scales of the flame.
See here
for more details.
Simulations
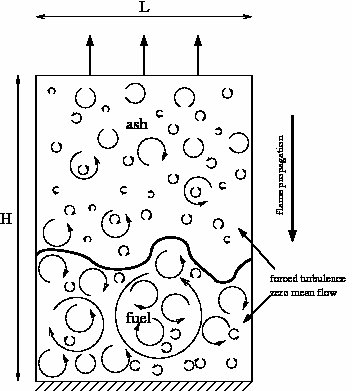
|
Three-dimensional simulations were run arranged with fuel below ash as shown in the figure on the left.
Periodic lateral boundary conditions were used, with a solid base and outflow at the top,
resulting in a downward propagating flame.
A high aspect ratio domain was used to allow the flame sufficient room to propagate.
A background turbulent field was maintained using a time-dependent zero-mean forcing term
consisting of a superposition of low wavenumber Fourier modes.
A range of Karlovitz numbers were simulated spanning several burning regimes. This was achieved by varying the
density of the fuel. Carbon at a density of 8x107g/cm3 has a laminar flame speed of 2.62x105 cm/s,
and a carbon width of 5x10-3 cm. At 1x107g/cm3, the laminar flame speed and width are 3.54x103 cm/s
and 2.31 cm respectively.
|
It was found that four to five cells across the carbon thickness (the shortest measure) was
sufficient to recover the correct laminar flame speed.
A base grid of 1282 in cross-section was used with one level of AMR to refine the flame,
giving an effective resolution of 2562 in cross-section.
The resulting domain had around 60 laminar flame widths across the domain, and ten integral length scales.
A total of five cases were simulated, the details of which are summarized in the table below:
| Case |
(a) |
(b) |
(c) |
(d) |
(e) |
| Fuel density (x107g/cm3) |
8 |
4 |
3 |
2 |
1 |
| Domain width (cm) |
0.32 |
2.0 |
4.6 |
9.5 |
150 |
| Domain height (cm) |
1.28 |
8 |
18.4 |
38.0 |
1500. |
| Turbulent intensity (x104cm/s) |
3.17 |
5.85 |
7.72 |
9.83 |
24.7 |
| Integral length scale (cm) |
0.032 |
0.2 |
0.46 |
0.95 |
15 |
| Karlovitz number |
0.0167 |
0.274 |
0.968 |
2.96 |
228 |
|
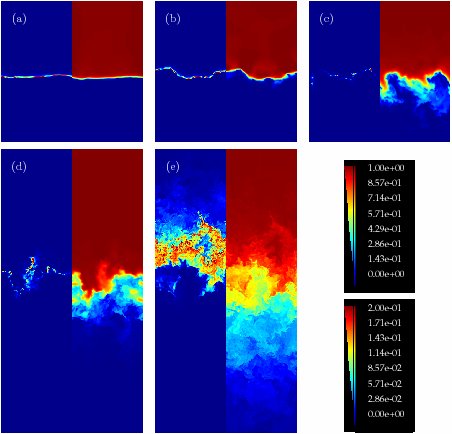
Instantaneous vertical slices through each flame. In each case, the left-hand panel is
fuel consumption rate and the right-hand panel is the temperature field.
Case (a) presents smooth and even burning, and is perturbed very little by the background turbulence.
The temperature profile remains sharp. In case (b), the flame surface has been deformed by
the turbulence. Both regions of enhanced burning and regions of decreased burning are observed,
and appear to be correlated with the curvature of the flame sheet. Specifically, enhanced burning
appears to occur where the center of curvature is within the fuel, and decreased when the center
of curvature is in the ash.
In case (e), a dramatically different burning mode is observed. The temperature mixed region
and the burning region are much broader. The burning appears to be much less intense and is restricted to
the high temperature end of the mixing zone. There is no well-defined flame surface, but a broad
flame brush.
|
|
|
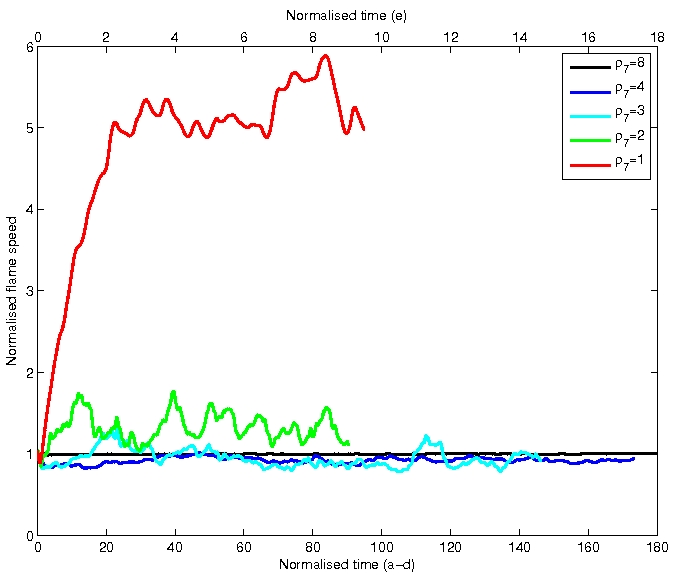
The turbulent flame speeds (defined to be the temporal derivative of the volume integrated fuel mass
divided by the fuel mass per unit area) for the five cases are shown on the left.
The combination of local extinction and enhancement in the low Karlovitz cases leads to a flame speed that remains close to the laminar value.
Despite the greatly reduced local burning in case (e), the overall turbulent burning speed is around 5 or 6 times the laminar flame speed
due to the greatly enhanced volume of fuel burning.
|
|
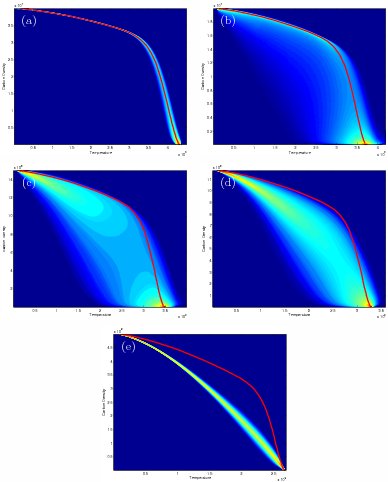
The figure on the right shows the joint probability density functions of fuel against temperature for the five cases.
The solid red line denotes the laminar flame distribution.
Because the turbulence does not have much effect on case (a), the turbulent burning path remains close to that of the laminar flame.
As the Karlovitz number is increased, there is a competition between thermal diffusion and turbulent mixing.
This leads to a decorrelation in the JPDFs for cases (b)-(d).
In case (e) the JPDF has collapsed to a single curve. This is because the flame is dominated by turbulent mixing, and thermal diffusion is having little effect.
|
|
The paper contains
much more detail, including isosurface analysis to correlate the local burning rate with curvature, and averaged profiles.
Any questions should be directed to Andy Aspden.
References
A. J. Aspden, J. B. Bell, M. S. Day, S. E. Woosley, M. Zingale,
"Turbulence-Flame Interactions in Type Ia Supernovae",
Astrophysical Journal, 689,
pp.1173-1185, December 20, 2008.
[ApJ]
[pdf]
[pdf2]
|




