CCSE Home

Overview

AMReX

People

Publications

Low Mach Number Approximations

Why Use A Low Mach Number Approach?

A large number of interesting fluid dynamical phenomena occur at low Mach numbers. For low speed flows in which the energy carried by the soundwaves is unimportant to the overall solution, numerical simulation based on the fully compressible form of the governing equations is inefficient, because of the need to follow the sound waves. For an explicit time-discretization (i.e., the new state is expressed solely in terms of the present state), stability considerations constrain the size of the allowable timesteps -- the CFL condition. A timestep is restricted such that information may only propagate across one zone in the computational grid per timestep.

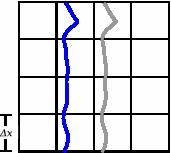In compressible flow, information propagates at the speeds: u, u + c, and u - c, where c is the sound speed. Mathematically the timestep restriction is expressed as

Δ t < min { Δ x / (|u| + c) }

For very low Mach number flows, this is

Δ t ~ Δ x / c

This means that for an interface moving at a Mach number M << 1, it takes 1/M timesteps for that interface to move just one zone!

Our desire is to reformulate the equations of hydrodynamics to filter out sound waves, while retaining the compressibility effects important to the problem at hand. This will result in a timestep constraint of the form

Δ t < min{ Δ x / |u| }

Therefore, our algorithm will require far fewer timesteps (~1/M fewer) to simulate low Mach number flows.

Instantaneous Equilibration -- An Example

As an example, we consider a set of reacting bubbles in a stratified stellar atmosphere. This plot of the Mach number demonstrates the effect of "instantaneous equilibration" in the low Mach number method.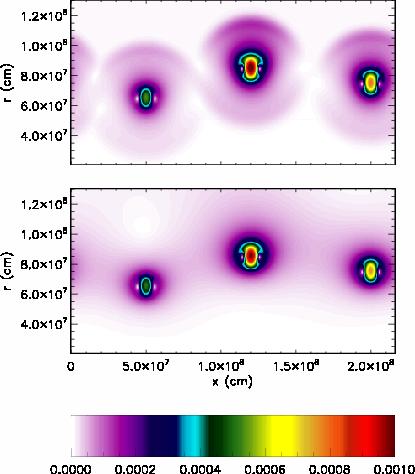

On the left, the top panel shows the fully compressible solution, while the bottom solution is calculated using a low Mach number method.

We initialize the calculation by placing three small temperature perturbations at varying heights in the atmosphere. In the compressible solution, a signal travels from each bubble at a finite speed. At this point in time (~0.04s after initialization), the bubbles are just starting to interact.

In the low Mach number solution, the acoustic signal travels infinitely fast, so the velocity field is already non-zero at points further than the physical sound travel time from each bubble. Because this flow is very subsonic, sound waves aren't important to the overall evolution, and the shapes and locations of the bubbles themselves are the same in the two calculations.

Different Low Mach Number Approximations

  • Incompressible hydrodynamics

    • The simplest low Mach number approximation is incompressible hydrodynamics. This approximation is formally the M → 0 limit of the Navier-Stokes equations. In incompressible hydrodynamics, the velocity satisfies a constraint equation

    ∇ ⋅ U = 0

    which acts to instantaneously equilibrate the flow, thereby filtering out soundwaves. The constraint equation implies that

    Dρ/Dt = 0

    which says that the density is constant along particle paths. This means that there are no compressibility effects modeled in this approximation.

  • Anelastic hydrodynamics

    • In the anelastic approximation small amplitude thermodynamic perturbations are carried with respect to a hydrostatic background. The density perturbation is ignored in the continuity equation, resulting in a constraint equation

    ∇ ⋅ (ρ0U) = 0

    This properly captures the compressibility effects due to the stratification of the background. Because there is no evolution equation for the perturbational density, approximations are made to the buoyancy term in the momentum equation.

  • Low Mach Number Combustion

    • In the low Mach number combustion model, the pressure is decomposed into a dynamic, π, and thermodynamic component, p0, the ratio of which is O(M2). The total pressure is replaced everywhere by the thermodynamic pressure, except in the momentum equation. This decouples the pressure and density and filters out the sound waves. Large amplitude density and temperature fluctuations are allowed. The only requirement is that the total pressure stay close to the background pressure, which is assumed constant for open domains. This requirement can be expressed as p = p0, and differentiating this along particle paths leads to a constraint on the velocity field:

    ∇ ⋅ U = S

    This looks like the constraint for incompressible hydrodynamics, but now we have a source term, S, representing the compressibility effects due to the energy generation and thermal diffusion.

    Since the background pressure is taken to be constant, we cannot model flows that cover a large fraction of a pressure scale height. However, this method is ideal for exploring the physics of flames, and is used in our work on laboratory-scale flames, small-scale flames and small-scale thermonuclear flames in Type I supernovae.

  • Low Mach Number Stellar Hydrodynamics

    • To model a full star we need to include compressibility effects from both heating and stratification. To derive this model, we begin with the low Mach number combustion model described above, but no longer assume that the background pressure is constant; instead, the background is hydrostatically stratified as in the anelastic approximation. This results in a constraint on the velocity field of:

    ∇ ⋅ ( β0U) = &beta0[ S - 1/(Γ1p0) ∂p0/∂t]

    Here, β0 is a density-like variable. Again, large amplitude density and temperature variations are allowed. The only restriction is that the pressure remain close to the background pressure. In the presence of heating, the star will expand, and therefore we need to evolve the background state in response to the local heating. This is the method, implemented in MAESTRO that we use to investigate ignition of Type Ia supernovae.



Both figures and much of the text are courtesy of Michael Zingale.