CCSE Home

CCSE Home

Overview

AMReX

People

Publications

Multiphase Flows and Complex Fluids

CCSE researchers are engaged in developing numerical algorithms and computational models to simulate the dynamics of complex fluids and multiphase flows whose mechanics are intricately governed with the evolution of the suspended microstructure. The examples of such fluids include particulate (granular) matter, particle-laden flows, and mixtures of rheologically-complex fluids. The computational approach involves integrating a particle-scale representation of these materials such as discrete element method (DEM), a coarse-grained representation such as particle-in-cell (PIC), and a continuum-scale partial differential equation (PDE) representation using the tools of adaptive mesh and algorithm refinement, and data-driven machine learning methods. The target applications include industrial technologies such as bioreactors, advanced manufacturing, and other DOE mission areas involving energy and environment. The overarching goal is to develop a multiscale modeling framework that can simulate a wide variety of these materials in complex flow scenarios, and is performant on manycore/GPU-based high performance computing (HPC) platforms.

Core Numerical Methologies:

  • CFD-DEM and CFD-PIC modeling of particle-laden multiphase flows

  • Mixture models for rheologically-complex non-Newtonian fluids

  • Polydisperse and polymorphic particle representation in multiphase flows

  • Immersed-boundary representation of particle suspensions

    • CCSE Members:

  • Ishan Srivastava

  • Aaron Lattanzi

  • Ann Almgren

  • Andy Nonaka

  • John Bell

    • CCSE researcher collaborate closely with National Technology Energy Laboratory (NETL) on the development and optimization of the MFIX-Exa software. Other AMReX codes used in this effort include the adaptive mesh, variable-density incompressible Navier-Stokes solver incflo and the fluctuating hydrodynamics code FHDeX.

    Current Projects:

    Theory and Modeling of Granular Matter

    Granular matter is prevelant in nature and industry, being only the second most widely-used material in industry after water. Their widespread occurence in nature ranges from soil to large-scale geophysical phenomena such as earthquakes and landslides, whereas they are also ubiquitous in pharamceutical, additive manufacturing and various energy-based industries. The mechanics of these materials is remarkably complex, and they can easily switch between solid-like, liquid-like and gas-like states. Currently, there exists no universal continuum model to predict their behavior in generalized loading conditions. While DEM simulations can accurately model granular matter, these methods are intractable at practical scales of interest.

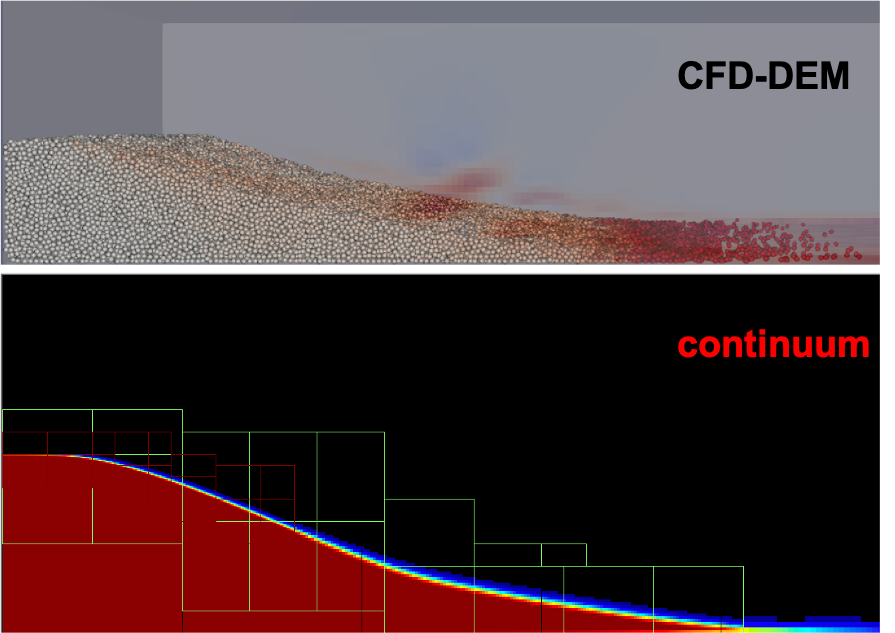
    CCSE researchers are engaged in developing advanced constitutive models for granular matter that can predict their response in arbitrary geometries and loading conditions. The strategy involves using DEM simulations to calibrate higher-order tensorial constitutive models that obey rotational and translational invariance, towards implementing these models in AMR-based incompressible and low-Mach number continuum fluid solvers. The details of the constitutive model are decribed in this paper and this paper.

    For more information, please contact Ishan Srivastava.

    Particle-Laden Multiphase Flows

    The dynamics of a mixture of particles and fluid exhibits a wide array of complex phenomena such as clustering and segregation, along with more exotic behavior such as shear thickening at large solid volume fractions. In collaboration with NETL, we are developing models for such multiphase flows that have several applications of interest to the DOE, including an ongoing investigation on modeling multiphase flows in bioreactors to achieve higher biomanufacturing efficiency (funded through the DOE's HPC4EnergyInnovation program by the AMMTO, EERE and IDEO offices).

    CCSE and NETL researchers have developed CFD-DEM and CFD-PIC based approaches for multiphase flow modeling within MFIX-Exa, where the solid phase is represented either by soft-sphere DEM representation (high fidelity, but expensive), or a coarse-grained PIC representation (lower fidelity, but scalable). Current developments include implementing complex interparticle DEM models with adhesion that are relevant in biomanufacturing, and incorporating higher-fidelity solid-phase constitutive models within the PIC represetation for such adhesive contacts. MFIX-Exa also has capabilities to model thermal transport and chemical reactions in multiphase flows, allows for resolving complex geometries using embedded boundary methods, and provides AMR capabilities.

    Details about MFIX-Exa have been described in this paper and this paper.

    For more information, please contact Ishan Srivastava, or Aaron Lattanzi.

    Polydispersity in Multiphase Flows

    In all but the most idealized conditions, multiphase flows exhibit significant polydispersity --- i.e., the particle characteristic size is described by a probability distribution other than a delta function (monodisperse). However, polydispersity will reduce the efficiency of Lagrangian particle solvers and the effect becomes increasly worse as the particle size ratio grows. More specifically, the construction of a neighbor list, for pair-wise interaction forces (collisions, etc.), must utilize a grid that is larger than the largest particle in the simulation. Consequently, many small particles, which cannot physically collide, will be added to the neighbor list. The artificially inflated neighbor list requires more operations and memory but also slows down the evolution of the particles' states since extra checks must be made when accumulating the net collisional force on a particle.

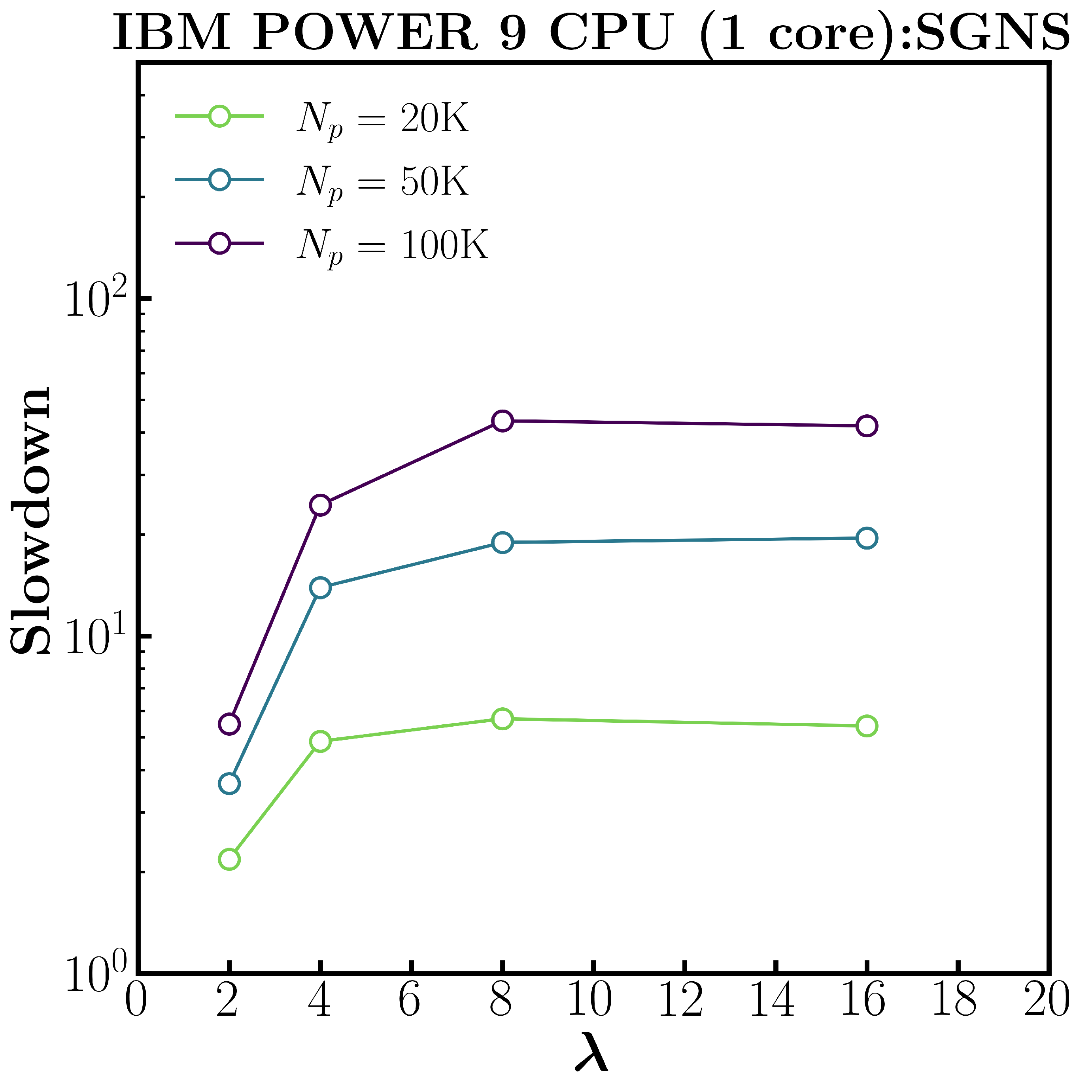
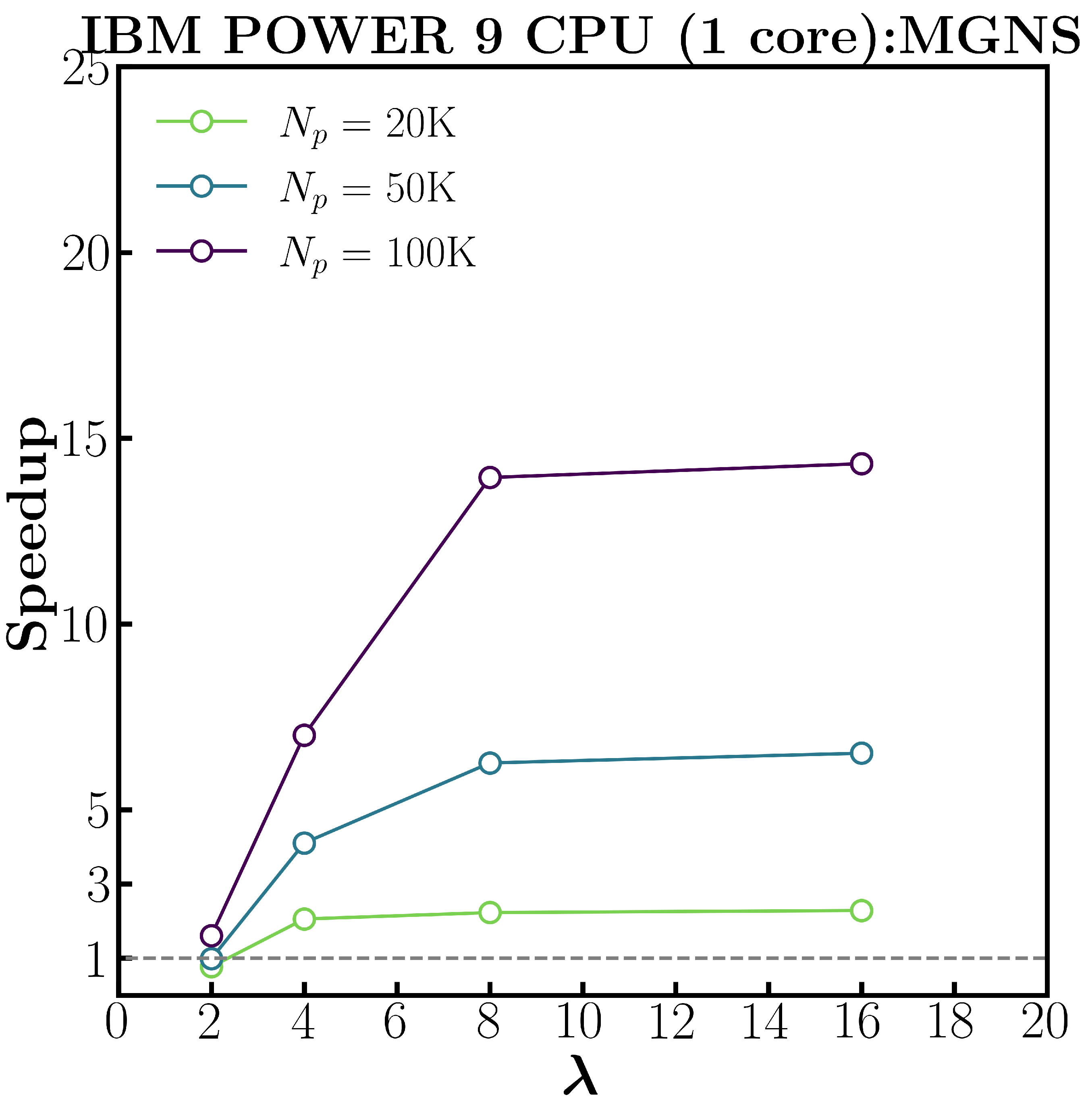
    The effect of particle size distribution on computational efficiency may be readily observed for the simple case of granular diffusion of a bidisperse mixture. The particles are seeded in three layers and given an initial granular temperature. As the simulation evolves, particles begin diffusing between one another and colliding. Compared to a monodisperse simulation with the same number of particles, the default single-grid neighbor list algorithm exhibits significant slowdown (nearly 40X for large size ratios and particle counts). By contrast, a new multi-grid neighbor list algorithm was implemented within AMReX (see Shire et al. (2021) for details) that yields significant speed up when compared to the single-grid neighbor list algorithm.

    For more information, please contact Aaron Lattanzi, Andrew Myers.

    Non-Newtonian Fluid Mechanics

    A defining feature of many complex fluids is the presence of a yield stress: for an insufficiently stressed material, they behave like an elastic solid, but once the yield stress is exceeded, they flow like a fluid. This broad class of fluids encompasses various materials of industrial and natural importance such as polymeric fluids, gels and viscoelastic suspensions. Unlike Newtonian fluids, the constitutive behavior of these fluids is highly complex, and they display intriguing phenomena such shear thickening, shear thinning, jamming, shear banding and normal stress differences.

    Previous work from our group has demonstrated simulations of viscoplastic fluids using a highly parallelizable structured adaptive mesh refinement method in AMReX-based code incflo. Further developments included modeling solid boundaries in viscoplastic fluids using embedded boundary methods. See more details in this paper and this paper.

    CCSE researchers are extending this framework by incorporating elastic effects through the implementation of elastoviscoplastic (EVP) models. The robustness of the numerical implementation will be extensively tested in various flow scenarios (such as Poiseuille and Couette flows) for a range Weissenberg and Bingham numbers. Another potential avenue for development involves implementing immersed boundary methods (IBM) to model solid particle suspensions in such complex non-Newtonian fluid matrix, which is an important precursor material for various DOE-relevant applications such as battery electrode manufacturing.

    For more information, please contact Ishan Srivastava.

    Data-Driven Modeling of Rheologically-Complex Microstructural Fluids

    In contrast to Newtonian fluids, complex fluids containing suspended microstructure exhibit complicated non-Newtonian rheology that is not well-described by a single governing equation. The macroscale dynamics of these materials is inherently complicated since it emerges from the dynamical evolution of the underlying microstructure. As such, a predictive high-fidelity modeling framework for complex fluids necessarily requires a multiscale approach where the microstructural evolution is upscaled to the constitutive response at continuum scales of practical interest. Scientific machine learning methods are ideally suited for enhancing such a multiscale approach by adaptively learning microstructural dynamics to predict the complex constitutive response at the continuum, particularly when traditional modeling methods are often computationally intractable.

    CCSE researchers are engaged in developing a multiscale modeling framework that explicitly couples particle-based and continuum simulations of complex fluids via active learning, thus providing a new predictive capability for domain scientists to conduct high-fidelity modeling of these materials at practical length scales.

    For more information, please contact Ishan Srivastava, and Andy Nonaka.