Machine Learning and Data-Driven Enhanced Modeling and Design
Researchers in CCSE are using machine learning and data-driven approach in numerous ways.
 Accelerate the time-to-solution of computationally-expensive kernels and PDE solvers.
As an outer-loop to accelerate predictive design for real-world systems.
On-the-fly learning strategies to provide algorithmic decisions.
Incorporating experimental data to make informative predictions.
Using pyTorch Models in AMReX for PDE acceleration
We have developed an interface to load a pyTorch-trained machine learning model into an AMReX simulation to replace a computational kernel.
A guided tutorial including a two-component beta decay system is available
HERE.
|
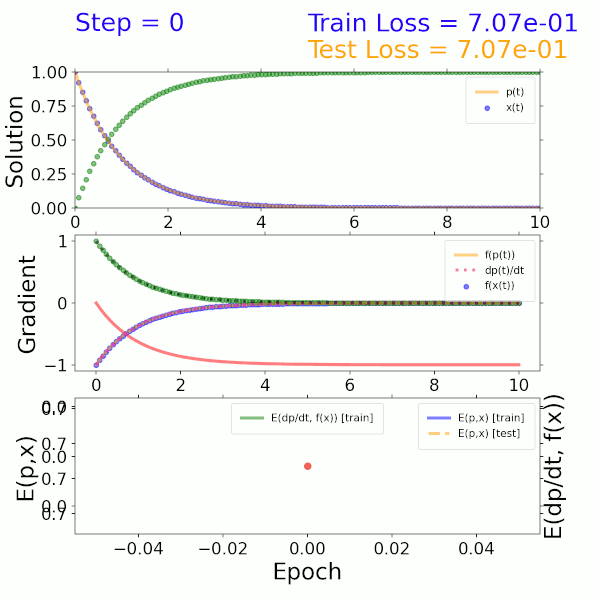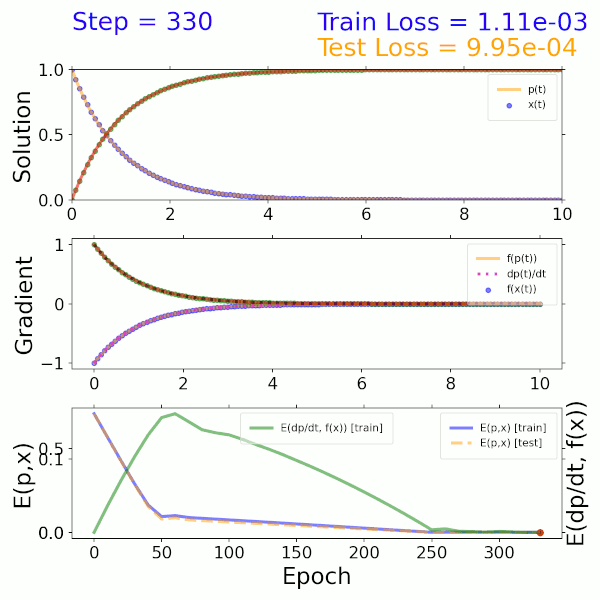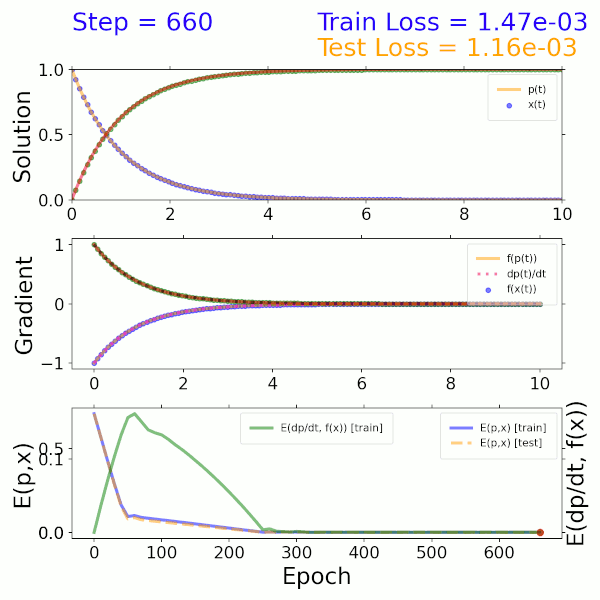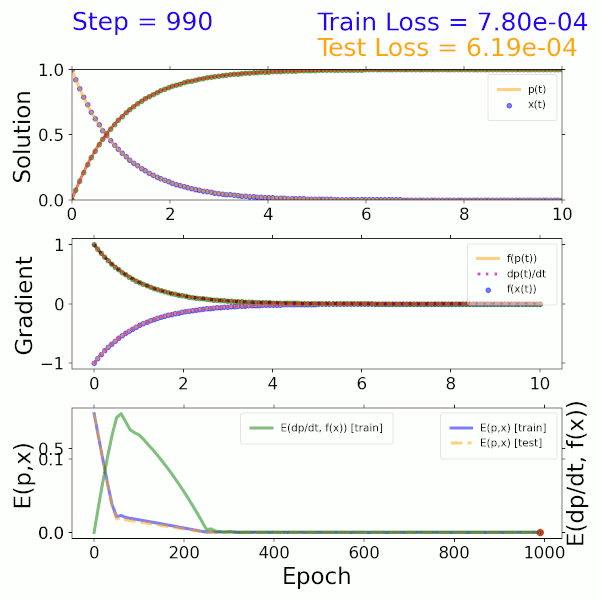
As a proof of concept, a surrogate model was trained using the solution to a two-component ODE system describing beta decay. The input is a time step and output is the solution representing the mass fractions of the two species. The model itself consists of a dense neural network (DNN) that imposes both mass fractions and mass fraction rates (gradients) as constraints in the loss function. As shown in the solution (top), gradient (middle), and error (bottom) plots on the left, this model converges to the exact solution after approximately 300 epochs.
|
Application: Astrophysical Reaction Networks
Our goal is to use a machine learning model to replace the reaction network in an astrophysical simulation.
We perform smallscale flame simulations with MAESTROeX using the aprox13 network in the
StarKiller Microphysics,
which is used in astrophysical simulations including stellar explosions (please refer to
Astrophysics and Cosmology
for more details)
Traditionally, we have used stiff ODE integrator for reactions, in which case the reactions dominate the total runtime.
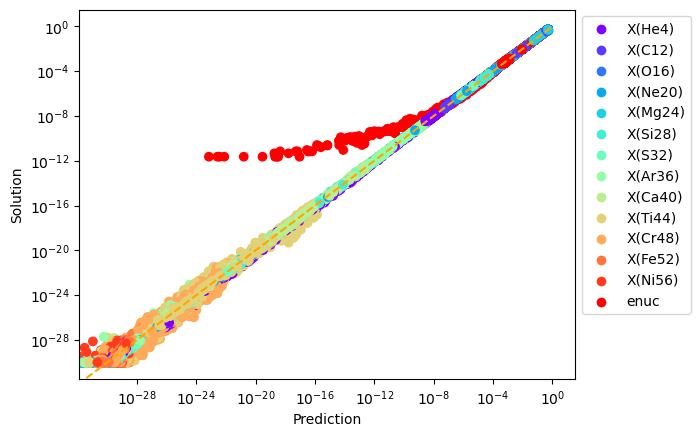
Preliminary tests have shown that the use of a ML model can reduce the runtime by an order of magnitude.
Below is a normalized plot of the prediction vs. solution for a number of species and the nuclear energy generation rate.
The model was trained by sampling a large fraction of cells in a traditional simulation, and generating the error plot with the unused training data.
Current development of machine learning capabilities for reaction networks can be found on our GitHub repo at
https://github.com/AMReX-Astro/ml-reactions.
For more information, please contact
Andy Nonaka
Data-Driven Modeling of Rheologically-Complex Microstructural Fluids
In contrast to Newtonian fluids, complex fluids containing suspended microstructure exhibit complicated non-Newtonian
rheology that is not well-described by a single governing equation. The macroscale dynamics of these materials is inherently
complicated since it emerges from the dynamical evolution of the underlying microstructure. As such, a predictive high-fidelity
modeling framework for complex fluids necessarily requires a multiscale approach where the microstructural evolution is upscaled
to the constitutive response at continuum scales of practical interest. Scientific machine learning methods are ideally suited for
enhancing such a multiscale approach by adaptively learning microstructural dynamics to predict the complex constitutive response
at the continuum, particularly when traditional modeling methods are often computationally intractable.
CCSE researchers are engaged in developing a multiscale modeling framework that explicitly couples particle-based and continuum
simulations of complex fluids via active learning, thus providing a new predictive capability for domain scientists to conduct
high-fidelity modeling of these materials at practical length scales.
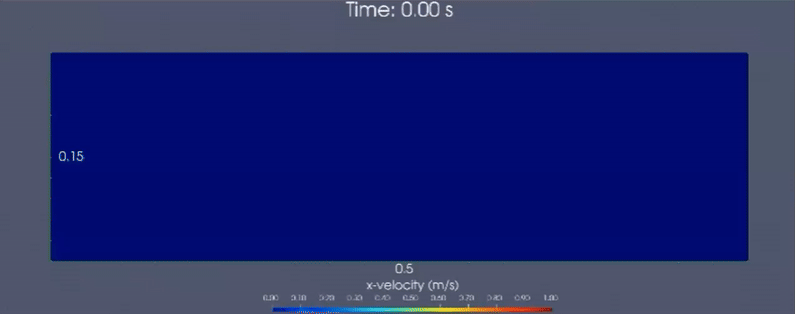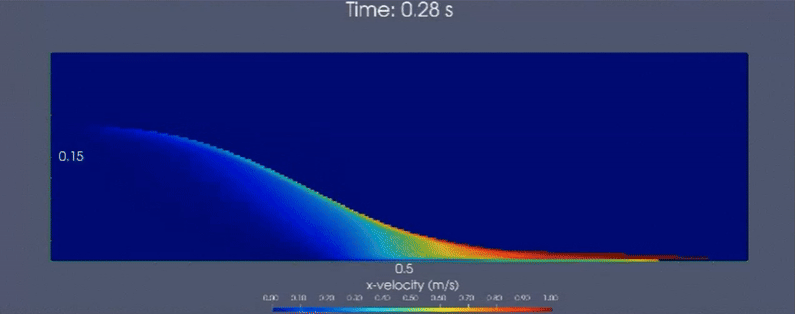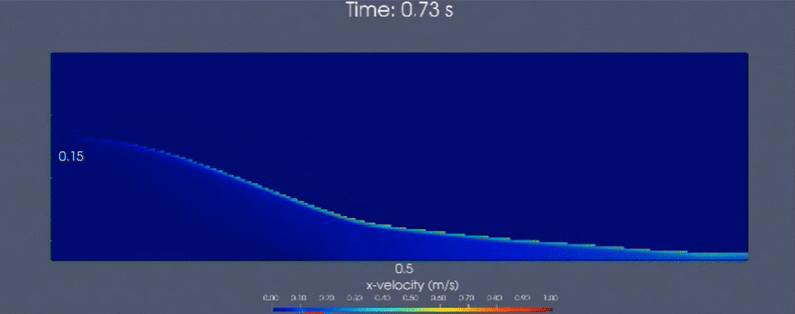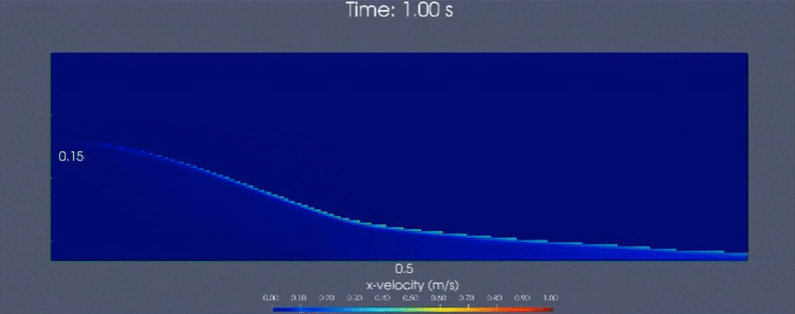
Below is a demonstrative multiscale-modeling framework based continuum simulation that leverages LAMMPS (particle-based)
and neural network ensembles to learn microstructural dynamics of a granular (glass beads) column collapse
that is initially held static. Horizontal velocity component is visualized.
For more information, please contact
Ishan Srivastava, and Andy Nonaka.
ML-based optimization of plasma-assisted chip fabrication
Nearly all semiconductor chips today are fabricated using plasma etching, a process that selectively removes materials from masked regions on a wafer. With shrinking feature sizes reaching physical limits, conventional 2D integration of dense transistor chips are no longer effective due to the associated complex fabrication processes and high defect/discard rate. Instead, a new class of energy-efficient devices (e.g., fin-type Field Effect Transistors, 3D NAND logic gates) are being designed with high-aspect ratio (HAR) 3D features. Therefore, chip manufacturers are now exploring new fabrication methods to etch these sub-nm features with deep trenches. By its nature, plasma processing creates a harsh environment that produces highly reactive radicals and energetic ions. A deliberate balance of their fluxes to the wafer is required such that the ions are energetic enough to provide selective, rapid, and reproducible etching, yet not so reactive or energetic to produce damage and defects. One of the main objectives of this work is to develop an ML-based optimization workflow using High Performance Computing (HPC) simulations to determine process parameters for optimum etch quality.
Towards an automated workflow for laser-plasma experiments using HPC simulations and ML
As part of a multi-area LDRD between PSA and CSA, we are developing an automated workflow to guide physical experiments of laser-plasma acceleration. The main objective is to perform simulations and experiments and train a neural net model using both sets of data, also learning the calibration between simulation and experimental data. The neural network will enable prediction of experiments, guiding experimentalists to determine operating conditions to maximize the quantity of interest. Our final goal is to automate the submission and analysis of simulations, generation of database from both simulation and experimental database, and training of the model, which will inform experimentalists of the optimum conditions using the updated model.
|
