CCSE Home

Overview

AMReX

People

Publications

MuMSS: Multiscale Modeling and Stochastic Systems

At macroscopic scales, fluid dynamics is governed by partial differential equations that characterize the behavior of the fluid in terms of smoothly evolving fields that represent density, momentum, and other characteristics of the fluid. However, at atomic scales fluids are discrete systems composed of individual molecules whose dynamics are governed by complex interaction potentials. The discrepancy between these two descriptions is manifest at the mesoscale. While it is possible to model a fluid using macroscopic field variables at the mesoscale, we know that they are no longer smooth fields; instead they fluctuate even for systems that are at thermodynamic equilibrium. The goal of the MuMSS team is to develop models and algorithms that can efficiently and accurately model complex fluids at the mesoscale

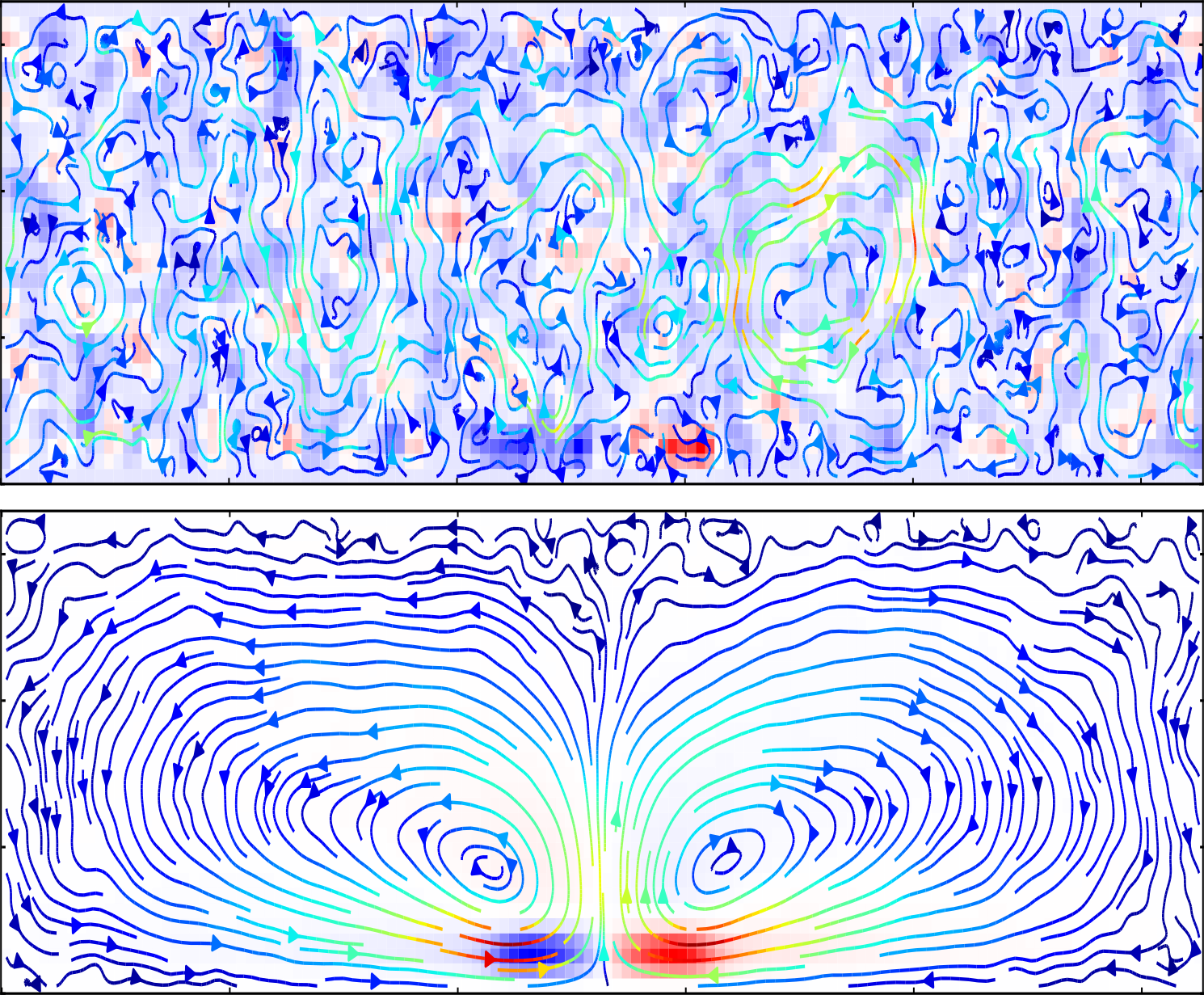
DISCOS: Discrete Ion Stochastic Continuum Overdamped Solvent

We have developed a methodology for the mesoscale simulation of strong electrolytes. The methodology is an extension of the fluctuating immersed-boundary approach that treats a solute as discrete Lagrangian particles that interact with Eulerian hydrodynamic and electrostatic fields. Hydrodynamic interactions are taken to be overdamped, with thermal noise incorporated using the fluctuating Stokes equation, including a "dry diffusion" Brownian motion to account for scales not resolved by the coarse-grained model of the solvent. Long-range electrostatic interactions are computed by solving the Poisson equation, with short-range corrections included using an immersed-boundary variant of the classical particle-particle particle-mesh technique. Also included is a short-range repulsive force based on the Weeks-Chandler-Andersen potential. This methodology is validated by comparison to Debye-Huckel theory for ion-ion pair correlation functions, and Debye-Huckel-Onsager theory for conductivity, including the Wien effect for strong electric fields. We refer to this approach as discrete ion stochastic continuum overdamped solvent (DISCOS). The algorithm is described in detail in this paper. For more information, please contact Daniel Ladiges and Galen Wang.

Room Temperature Ionic Liquids

We have developed a new mesoscale model for ionic liquids based on a low Mach number fluctuating hydrodynamics formulation for multicomponent charged species. The low Mach number approach eliminates sound waves from the fully compressible equations leading to a computationally efficient incompressible formulation. The model uses a Gibbs free energy functional that includes enthalpy of mixing, interfacial energy, and electrostatic contributions. We have calibrated our model using parameters for [DMPI+][F6P-], an extensively-studied room temperature ionic liquid (RTIL), and have numerically demonstrated the formation of mesoscopic structuring at equilibrium in two and three dimensions. In simulations with electrode boundaries, the measured double layer capacitance decreases with voltage, in agreement with theoretical predictions and experimental measurements for RTILs. The results of our study are described in detail in this paper. For more information, please contact John Bell and Andy Nonaka.

Compressible Fluctuating Hydrodynamics for Transpiration of Gas Mixtures across Membranes

We have developed a methodology for mesoscale simulations of multicomponent gases based on a compressible fluctuating hydrodynamics (FHD) formulation. Both cell-centered and staggered discretizations of the stochastic PDEs are implemented in AMReX along with capabilities for GPU optimization. We are currently using this methodology to simulate transpiration of gas mixtures across nanoporous membranes with applications in gas separation technologies. We have implemented a Langevin model for fluctuating effusive fluxes of mass, momentum and energy across the membrane, along with reservoirs to impose a concentration gradient. The methodology is being validated against a discrete simulation Monte Carlo (DSMC) implementation of the gas mixture effusion. In previous work, we have simulated the effusion of a single component gas held at a nonequilibrium steady state by imposing a temperature gradient through isothermal walls using both DSMC and FHD, along with Master equation and Langevin models for effusion. Good agreement was observed between DSMC and FHD with the latter showing a significant advantage in computational speed. Furthermore, the principal effect of transpiration was found to be a suppression of long-ranged hydrodynamic correlations, an outcome largely explained by a reduction in the temperature gradient due to the membrane. The results of the study are described in detail in this paper. For more information, please contact Ishan Srivastava and Daniel Ladiges

Coupling Fluctuating Hydrodynamics With Surface Chemistry

An increasing number of micro and nanoscale technologies rely on heterogeneous catalysis, where reacting chemical components can exist in both a gaseous phase and on adjoining solid surfaces. To properly design such devices, it is critically important to understand chemistry on the solid interface as well as the transport of these components in the gas phase. Furthermore, for the design of increasingly smaller technologically innovative devices, a correct description of thermal fluctuations in both phases is crucial. We have developed a computationally efficient simulation methodology that can accurately describe both phases and their coupling. To describe transport behavior in the bulk fluid region at small scales, we use a fluctuating hydrodynamics (FHD) approach, whereas a kinetic Monte Carlo (KMC) method is used to describe stochastic chemistry on the surface. For more information, please contact Changho Kim.

I. Srivastava, D. R. Ladiges, A. Nonaka, A. L. Garcia, J. B. Bell, Staggered Scheme for the Compressible Fluctuating Hydrodynamics of Multispecies Fluid Mixtures, Physical Review E, 107, 015305, 2023. [arxiv] [doi]

D. R. Ladiges, J. G. Wang, I. Srivastava, S. P. Carney, A. Nonaka, A. L. Garcia, A. Donev and J. B. Bell, Modeling Electrokinetic Flows with the Discrete Ion Stochastic Continuum Overdamped Solvent Algorithm, Physical Review E, 106, 035104, 2022. [doi]

Robin J Dolleman, Debadi Chakraborty, Daniel R Ladiges, Herre SJ van der Zant, John E Sader, and Peter G Steeneken, Squeeze-film effect on atomically thin resonators in the high-pressure limit, Nano Letters, 2021. [doi]

D. R. Ladiges, S. P. Carney, A. Nonaka, K. Kymko, G. C. Moore, A. L. Garcia, S. R. Natesh, A. Donev and J. B. Bell, A Discrete Ion Stochastic Continuum Overdamped Solvent Algorithm for Modeling Electrolytes, Physical Review Fluids, 6(4), 044309, 2021. [arxiv]

K. Klymko, S. P. Carney, A. Nonaka, A. L. Garcia, and J. B. Bell, A Low Mach Number Fluctuating Hydrodynamics Model For Ionic Liquids, Phys. Rev. Fluids, 5, 9, 2020. [arxiv]

Nicholas Z. Liu, Daniel R. Ladiges, Jason Nassios, and John E. Sader, Acoustic flows in a slightly rarefied gas, Physical Review Fluids, 5(4), 043401, 2019. [doi]

Yong Shi, Daniel. R. Ladiges, and John E. Sader, Origin of spurious oscillations in lattice Boltzmann simulations of oscillatory noncontinuum gas flows, Physical Review E, 100(5), 053317, 2019. [doi]

D. R. Ladiges, A. J. Nonaka, J. B. Bell, and A. L. Garcia, "On the Suppression and Distortion of Non-Equilibrium Fluctuations by Transpiration," Phys. Fluids, 149, 052002, 2019. [doi]

A. Donev, A. J. Nonaka, C. Kim, A. L. Garcia and J. B. Bell, "Fluctuating hydrodynamics of electrolytes at electroneutral scales," Phys. Rev. Fluids. 4, 4, 2019. [link]

A. Donev, A. L. Garcia, J.-P. Péraud, A. J. Nonaka and J. B. Bell, "Fluctuating Hydrodynamics and Debye-Hückel-Onsager Theory for Electrolytes," submitted for publication [arxiv]

C. Kim, A. Nonaka, J.B. Bell, A.L. Garcia, and A. Donev, "Fluctuating hydrodynamics of reactive liquid mixtures," J. Chem. Phys. 149, 084113, 2018. [doi] [arxiv]

J-P. Péraud, A. Nonaka, J. B. Bell, A. Donev, and A. L. Garcia, "Fluctuation-Enhanced Electric Conductivity in Electrolyte Solutions," P. Natl. Acad. Sci. USA, 114, 41, 2017. [doi] [arxiv]

C. Kim, A. Nonaka, J. B. Bell, A. L. Garcia, and A. Donev, "Stochastic Simulation of Reaction-Diffusion Systems: A Fluctuating-Hydrodynamics Approach," J. Chem. Phys. 146, 124110, 2017. [doi] [arxiv]

J-P. Péraud, A. Nonaka, A. Chaudhri, J. B. Bell, A. Donev, and A. L. Garcia, "Low Mach Number Fluctuating Hydrodynamics for Electrolytes," Phys. Rev. Fluids 1, 074103, 2016. [doi] [arxiv]

A. K. Bhattacharjee, K. Balakrishnan, A. L. Garcia, J. B. Bell, and A. Donev, "Fluctuating Hydrodynamics of Multispecies Reactive Mixtures," J. Chem. Phys. 142, 224107, 2015. [doi] [arxiv]

A. Donev, A. Nonaka, A. K. Bhattacharjee, A. L. Garcia, and J. B. Bell, "Low Mach Number Fluctuating Hydrodynamics of Multispecies Liquid Mixtures," Phys. Fluids 27, 037103, 2015. [doi] [arxiv]

A. Nonaka, Y. Sun, J. B. Bell, and A. Donev, "Low Mach Number Fluctuating Hydrodynamics of Binary Liquid Mixtures," Comm. App. Math. Comp. Sci. 10, 163-204, 2015. [doi] [arxiv]

A. Chaudhri, J. B. Bell, A. L. Garcia, and A. Donev, "Modeling Multi-Phase Flow Using Fluctuating Hydrodynamics", Phys. Rev. E 90, 033014, 2014. [doi] [arxiv]

M. Cai, A. Nonaka, B. E. Griffith, J. B. Bell, and A. Donev, "Efficient Variable-Coefficient Finite-Volume Stokes Solvers," Commun. Comput. Phys. 16, 1263-1297, 2014. [doi] [arxiv]

A. Donev, A. Nonaka, Y. Sun, T. Fai, A. Garcia, and J. B. Bell, "Low Mach Number Fluctuating Hydrodynamics of Diffusively Mixing Fluids," Comm. App. Math. Comp. Sci. 9, 47-105, 2014. [doi] [arxiv]

K. Balakrishnan, A. Garcia, A. Donev, and J. B. Bell, "Fluctuating Hydrodynamics of Multispecies Nonreactive Mixtures," Phys. Rev. E 89, 013017, 2014. [doi] [arxiv]

F. Balboa Usabiaga, J. B. Bell, R. Delgado-Buscalioni, A. Donev, T. Fai, B. Griffith, and C. Peskin, "Staggered Schemes for Fluctuating Hydrodynamics," Multiscale Model. Simul. 10, 1360-1408, 2012. [doi] [arxiv]

K. Balakrishnan, J. B. Bell, A. Donev, and A. Garcia, "Fluctuating Hydrodynamics and Direct Simulation Monte Carlo," 28th International Symposium on Rarefied Gas Dynamics, AIP Conf. Proc. 1501, 695-704, 2012. [pdf]

A. Garcia, A. Donev, J. B. Bell, and B. Alder, "Hydrodynamic Fluctuations in a Particle-Continuum Hybrid for Complex Fluids," 27th International Symposium on Rarefied Gas Dynamics, AIP Conf. Proc. 1333, 551-556, 2011. [pdf]

A. Donev, A. de la Fuente, J. B. Bell, and A. L. Garcia, "Enhancement of Diffusive Transport by Nonequilibrium Thermal Fluctuations," JSTAT 2011, P06014, (2011). [doi] [arxiv]

A. Donev, A. de la Fuente, J. B. Bell, and A. L. Garcia, "Diffusive Transport by Thermal Velocity Fluctuations," Phys. Rev. Lett. 106, 204501, 2011. [doi] [arxiv]

A. Donev, J. B. Bell, A. L. Garcia, and B. J. Alder, "A Hybrid Particle-Continuum Method for Hydrodynamics of Complex Fluids," Multiscale Model. Simul. 8, 871-911, 2010. [doi [arxiv]

A. Donev, E. Vanden-Eijnden, A. Garcia, and J. Bell, "On the Accuracy of Explicit Finite-Volume Schemes for Fluctuating Hydrodynamics," Comm. App. Math. Comp. Sci. 5, 149-197, 2010. [doi] [arxiv]

J. B. Bell, A. L. Garcia, and S. A. Williams, "Computational Fluctuating Fluid Dynamics," ESAIM: Mathematical Modelling and Numerical Analysis 44, 1085-1105, 2010. [doi] [pdf]

A. Donev, A. L. Garcia, and B. J. Alder, "A Thermodynamically-Consistent Non-Ideal Stochastic Hard Sphere Fluid," J. Stat. Mech., P11008, 2009. [doi] [arxiv]

S. A. Williams, J. B. Bell, and A. L. Garcia, "Algorithm Refinement for Fluctuating Hydrodynamics," Multiscale Model. Simul. 6, 1256-1280, 2008. [doi] [pdf]

J. B. Bell, A. L. Garcia, and S. A. Williams, "Numerical Methods for the Stochastic Landau-Lifshitz Navier-Stokes Equations," Phys. Rev. E 76, 016708, 2007. [doi] [arxiv]

J. B. Bell, J. Foo, and A. L. Garcia, "Algorithm Refinement for the Stochastic Burgers' Equation," J. Comp. Phys. 223, 451-468, 2007. [doi] [pdf]

A. L. Garcia, J. B. Bell, W. Y. Crutchfield, and B. J. Alder, "Adaptive Mesh and Algorithm Refinement Using Direct Simulation Monte Carlo," J. Comp. Phys. 154, 134-155, 1999. [doi] [ps.gz]